Verification & Validation — Lesson 8
This section contains a few formulas, which made the listed assumptions, found in the Pre-Analysis & Start-Up page.
The analytical formula for computing the radius of contact zone (a) is given as follows:
The following command for the computation of the contact area can be downloaded here.
- This command was generously provided by Mr. Sean Harvey. (Lead Technical Services Engineer at Ansys.)
| Theoretical | Numerical | Relative Error(%) | |
|---|---|---|---|
| Contact radius, a [mm] | 1.00964 | 1.02517 | 1.538 |
Using this value of contact radius, we can also compute the normal pressured induced at the contact zone. Theoretically, the maximum pressure (pmax) is induced along the y-axis, as expected, and is given by the following formula: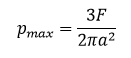
| Theoretical | Numerical | Relative Error(%) | |
|---|---|---|---|
| Max Pressure, Pmax [MPa] | 88.290 | 81.094 | 8.151 |
Furthermore, we can derive the following formula for the normal stresses σz and σr = σθ along the z-axis.
Here we note that the principal normal stresses σ1 = σ2 = σr = σθ since the out-of-plane shear stresses, τrz = τθz = 0 and σ3 = σz. And we can deduce that τmax = |τ1|=|τ2|=|(σ1-σ2) / 2|. The effective stress (using the von-Mises criterion) along the y-axis can be computed as the following:
Lastly, we also confirm that the applied load at the top vertex of the sphere matches our numerical contact pressure, integrated along the interface.
| Mesh Size [m] | 2.00E-04 | 1.00E-04 | 9.00E-05 | Theoretical |
|---|---|---|---|---|
| Force Reaction [N] | 187.95 | 188.32 | 188.52 | 188.50 |
| Relative Error [%] | 0.29 | 0.09 | 0.01 | 0.00 |


