Verification & Validation — Lesson 8
Created by Sebastien Lachance-Barrett
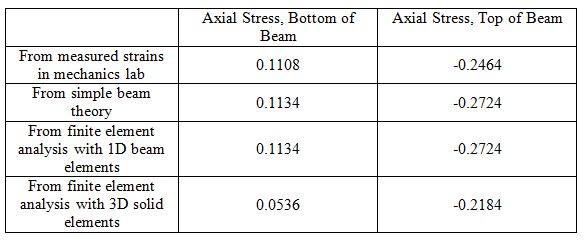
Reasons for this disagreement are discussed in the text in Example 4.1. Relatively substantial differences in stress can result from differences in strain that are orders of magnitude smaller. Such differences in strain can result from Poisson effects when all nodes are constrained through the thickness of the cross-section. When out-of-plane curvature results due to Poisson effects (see Figure 4.9 of the text), the constraint of all nodes along the knife-edge may over-constrain the cross-section. As a result, one can relax the simple support constraint in three dimensions by constraining ONLY a subset of nodes along the knife-edge to allow this out-of-plane curvature to occur.
When this is done, the results seem more reasonable:
The loads and boundary conditions here were not originally placed along the neutral axis as prescribed by Euler-Bernoulli beam theory, yet the theory performs reasonably well when the end constraints are relaxed to allow for out-of-plane curvature as might be expected in this case. Further alternative considerations for relevant boundary conditions are considered in the Exercises.