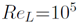Exercises — Lesson 11
Exercise 1
Simulate the laminar boundary layer over a flat plate using Fluent for a Reynolds number ![]() where
where 
Change the value of the coefficient of viscosity µ from the tutorial example to get , keeping all other parameters the same. After changing the coefficient of viscosity, rerun the solver for the mesh that was created in Lesson 4.
While developing boundary-layer theory, Prandtl made the following key arguments about the boundary-layer flow to simplify the Navier-Stokes equations:
![]()
Streamwise velocity gradients ≪ Transverse velocity gradients, for instance,

- Since we are solving the Navier-Stokes equations, we can use the Fluent solution to check the validity of the above two essential features of boundary layers. Consider the solution at x = 0.5 and x = 0.7 and make plots of appropriate profiles to check the validity of these two features. Make one figure to illustrate each feature. Choose the upper limit of your abscissa (vertical axis) such that you can clearly see the variation within the boundary layer (the flow outside the boundary layer is not very interesting in this case).
- For the Fluent solution, plot the u-velocity profiles (y vs. u) at x=0.5, 0.7, and 0.9 in the same figure. Briefly comment on the change in the velocity profile with x.
- Prandtl's student Blasius deduced that the velocity profiles in a flat plate boundary layer obey the similarity principle, i.e., if rescaled accordingly, they should collapse to a single curve. Re-plot the profiles from exercise 2 in terms of the Blasius variables
 in a different figure. Also plot the corresponding values from the Blasius solution in this figure. How well does the Fluent solution obey the similarity principle?
in a different figure. Also plot the corresponding values from the Blasius solution in this figure. How well does the Fluent solution obey the similarity principle?
Exercise 2 — Quantitative Explanation of the Velocity Profile Overshoot
First-order boundary layer theory says that the flow outside of the boundary layer remains undisturbed, but we see that Fluent predicts an overshoot in the velocity due to the presence of the boundary layer since the flow accelerates. (For a more in depth explanation see the video explaining this here.) This acceleration and overshoot can be attributed to the displacement thickness of the boundary layer. In this exercise, modify the flat plate to account for this displacement thickness, plot the velocity at the outlet, and compare your results to the flat plate solution from the tutorial.

You will need to create a geometry file that can imported into Ansys DesignModeler. There are several ways to do this, but one way is to create the curve for the boundary layer displacement thickness in Excel and then connect the appropriate points together. Remember, DesignModeler takes in "zones" which will be your first column so that it can identify the edges in the geometry. The second column will be the points in those zones that DesignModeler connects together. The third, fourth, and fifth columns are your x, y, z points, respectively. Since this problem is 2D, the z column should be all 0.
For example: if you wanted to make a square with a height and length of 1, your file would look like this:

Flow outside of the boundary layer is inviscid and you will need to change this in your Model Setup.
Once you have run the simulation, you should see something similar to the plot below:

What happens to the velocity at the outlet when we account for the displacement thickness? Compare your Fluent results from this exercise to the results from the tutorial and the Blasius solution. What is happening to the velocity profile at the outlet?
Instructions for Cornell students
MAE 3240/4230/5230: You DO NOT need to do this section.